Cet article présente, en résumé, les savoirs théoriques et les informations qui ont été transmis lors de la formation Enseigner la géométrie à l’école qui s’est tenue le mercredi 8 mars 2023 dans les locaux de l’école F. Buisson – Lamartine à Hazebrouck.
Qu’est-ce que la géométrie ?
Etymologiquement, le géomètre est celui qui mesure la Terre. La plupart des savoirs géométriques que nous utilisons à l’école nous viennent de l’Antiquité et datent de plus de 2 000 ans. C’est Euclide qui, vers – 300 avt. J.C., a théorisé ces savoirs en axiomes et en théorèmes dans les Eléments. On parle donc de géométrie euclidienne. Mais il existe d’autres géométries, la géométrie sphérique, la géométrie absolue, la géométrie hyperbolique, la géométrie des origami japonais qui a ses propres théorèmes, dont certains sont encore à démontrer. Même s’il est très ancien, le savoir géométrique universel évolue encore de nos jours. Mais à l’école, nous n’en sommes pas là.
Pourquoi faire de la géométrie à l’école ?
- A l’école primaire, la géométrie, c’est une modélisation (comprendre : “une mathématisation”) de l’espace. On y enseigne une géométrie qui servira à résoudre des problèmes de la vie courante, des problèmes ayant trait à l’espace. Avec une culture, un vocabulaire, des pratiques que l’on voudrait partagés par tous.
- La géométrie est aussi un pont entre différentes disciplines : elle donne du sens aux opérations mathématiques, un autre sens aux nombres, elle est à la croisée des arts visuels, de la géographie, de l’EPS et des mathématiques.
- Enfin, on fait de la géométrie à l’école pour apprendre à regarder et à raisonner, à penser, ce qui, dans la vie, n’est pas toujours inutile.
Une réponse plus exhaustive à la question posée est formulée dans cette ressource qui accompagne les programmes de 2015 : Espace et géométrie au Cycle 3. C’est d’ailleurs ce document qui a servi de point de départ pour la fabrication de la formation de ce jour. Il peut ne pas être inutile, même aux enseignantes et aux enseignants de cycle 2, de le consulter. J’en propose d’ailleurs un résumé ici : Espace et géométrie.
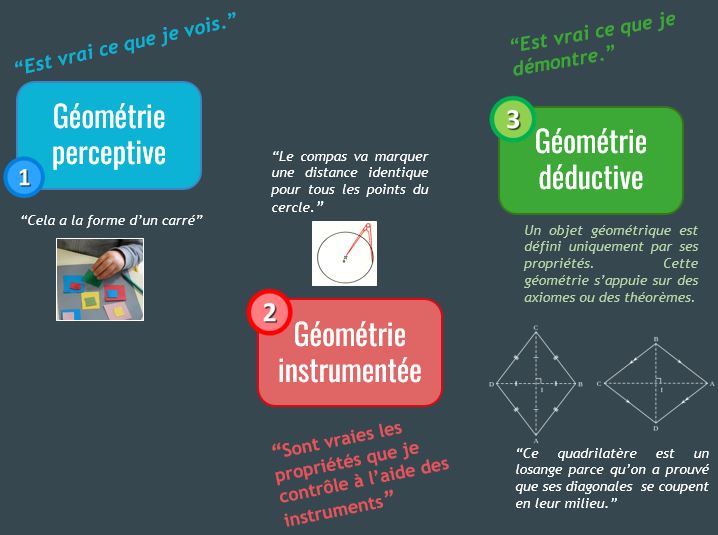
Trois grandes étapes pour aborder la géométrie à l’école
On peut considérer que la première des géométries de l’école, celle de la perception, est plutôt du ressort du cycle 1, la deuxième, la géométrie instrumentée, serait plutôt travaillée aux cycles 2 et 3, et la géométrie déductive réservée au collège (fin de cycle 3 et cycle 4). Mais ce découpage est artificiel et grossier. En fait, ce qui va changer, d’un cycle à l’autre, ce sont les mots et le langage utilisés pour décrire, nommer, les formes que l’on perçoit et en faire des figures géométriques.
Car le passage d’un espace vécu et perçu de manière sensible vers un espace conçu et pensé en objets mathématiques se fait par le biais de la verbalisation en faisant de nombreux allers-retours du monde réel au monde mathématique.
La géométrie, à l’école, est une géométrie du faire. Pour l’enseigner, il importe donc de faire faire de la géométrie : ce n’est pas une “leçon de choses” où l’on se contenterait d’observer et de décrire des faits, puis de mémoriser un vocabulaire et des définitions. Les concepts géométriques, à l’école, s’expérimentent dans l’action. Cela suppose le développement de 5 grandes compétences.
Cinq compétences pour faire de la géométrie
- Des compétences visuelles : reconnaissance des figures, des propriétés, interprétation des images. L’œil du géomètre n’est pas celui de tout le monde.
- Des compétences langagières : connaissance des mots pour dire ce que l’on voit, ce que l’on fait.
- Des compétences logiques : sérier, classer, ordonner, comparer, trouver des régularités, déduire des informations.
- Des compétences en dessin : même si, comme on le pense souvent, à tort, la précision n’est pas l’alpha et l’oméga de la géométrie. La représentation d’un objet géométrique n’est jamais l’objet géométrique lui-même, elle est toujours imparfaite. Mais la communication, en géométrie, passe par le dessin.
- Des compétences appliquées : la géométrie est utile pour construire et fabriquer des objets concrets.
Une séquence d’apprentissage en géométrie devrait donc proposer ces 5 activités :
- Reconnaitre
- Décrire
- Reproduire
- Construire
- Transformer
En conclusion

Contenu des trois ateliers
Atelier 1 – MANIPULER avec Hélène Varin
Formes géométriques à l’école maternelle
Atelier 2 – DECRIRE avec Pierre Snaet
Retrouvez ici le logiciel et l’application qui ont servi à l’animation à laquelle vous avez participé.
Le Village géométrique – Académie de Grenoble
Atelier 3 – RAISONNER avec Frédéric Paris
Les figures téléphonées, fiche de préparation
Et après
Et après ?
Nous vous invitons à tester dans vos classes, si vous le souhaitez et si cela ne perturbe pas complétement votre programmation annuelle, les activités qui ont été présentées dans les ateliers. Un temps sera consacré, lors de la deuxième session de formation qui se tiendra le mercredi 31 mai 2023, à vos retours.
Frédéric Paris a créé un espace collaboratif sur TRIBU pour que vous puissiez y poster vos contributions, propositions ou témoignages. Vous avez du recevoir une invitation à rejoindre cet espace. Vous pouvez y accéder à tout moment via Eduline/Applications/Formation et ressources/Plate-forme collaborative : Tribu/ (cliquez sur Connesion puis) Géométrie Dk Haz
S’il y a des remarques, des questions ou des améliorations à proposer, vous pouvez nous les faire parvenir par courriel à pierre.snaet@ac-lille.fr ou à frederic.paris@ac-lille.fr ou encore à helene.varin@ac-lille.fr .