Samedi 28 novembre, début de week-end studieux pour les enseignants de cycle 1 de la circonscription. Rassemblés dans la salle des Augustins, ils ont pu suivre la conférence qu’y donnait Fabien Emprin, enseignant chercheur de l’Université de Reims.

Le propos portait sur La construction du nombre à l’école maternelle et notamment sur les différentes façons d’aider les élèves à construire le concept de nombre en les mettant face à des problèmes ouverts.

Lors de cette conférence, M. Emprin apporta des réponses à ces grandes questions que se pose chaque enseignant de l’école maternelle : qu’est-ce que compter ? Qu’est-ce que le concept de quantité ? Qu’est-ce qu’un nombre et à quoi sert celui-ci ? À partir de quand peut-on dire qu’un élève connaît le nombre ? Chaque réponse étant éclairée par des allers-retours entre la théorie universitaire et les activités en classe.

Préambule : méfions-nous des automatismes !

Première réflexion à propos des automatismes développés par les élèves : un élève bien particulier, le singe qui parvient en un temps record à ranger les neuf premiers chiffres apparus devant ses yeux quelques secondes seulement sait-il compter ? La réponse, évidemment, est non, car ce dernier – si doué soit-il pour cette activité – ne lui donne pas le sens que le cerveau humain lui donne. En tant qu’enseignants, nous devons apprendre à nous méfier de certaines compétences qu’acquièrent nos élèves par automatisme et qui peuvent laisser croire que… Mais en fait non !

De même, multiplier par 10, c’est rajouter un zéro, tout le monde le sait ! Ainsi l’élève qui, en cycle 2, résout sans problème des multiplications par 10, écrit-t-il sans sourciller, arrivé au cycle 3, que 12,5 x 10 font 12,50, ou bien 120,5… Méfions-nous des automatismes qui ne s’accompagnent pas forcément de la construction du concept associé ! Là encore sens et automatisme ne sont pas liés !

Mais les automatismes sont néanmoins nécessaires à l’apprentissage : ils permettent d’alléger la mémoire de travail de l’élève. (Cf. Le paradoxe de l’automatisme de Butlen et Pézard, in Le nombre au cycle 2, éditions Canopé – téléchargement gratuit). Le travail de l’enseignant sera donc d’amener les élèves vers l’automatisme une fois qu’ils auront saisi l’entièreté du sens de l’activité, quand ? On en peut pas le décider de manière empirique, pour tous les élèves. Comment ? Par l’entraînement, car le passage à l’automatisme n’est pas automatique !

Qu’est-ce que compter ?

Compter, c’est dénombrer, c’est à dire extraire la quantité d’une collection.

Il y a trois façons de dénombrer une collection :

• le subitizing (qui ne fonctionne malheureusement que pour les quantités de 1 à 3)
• le comptage de un en un, appeler aussi énumération ou dénombrement (avec les nuances que l’on connaît entre ces deux termes)
• le calcul

La quantité d’une collection n’est qu’une des qualités de celle-ci, elle est indépendante de la taille, de la forme, de la couleur… Cela suppose, pour qui veut compter, une certaine capacité d’abstraction. C’est celle que découvrirent les premiers hommes quand, pour se remémorer leurs chasses, ils sont passés, vers 15 000 avant JC, de la représentation de scènes de chasses sur les parois de leurs grottes à quelques encoches taillées dans un bois de cerf, en faisant ainsi abstraction de toutes les informations autres que la quantité (taille des proies, couleur, aspect…)

Comment amener nos élèves à faire ce chemin que firent avant nous les hommes du paléolithique ? M. Emprin et son équipe proposent l’activité Passe-moi le sel décrite dans ces deux vidéos à télécharger : Passe-moi le sel ! et Passe-moi le sel ! (2).

Remarque : Dans cette vidéo, la mise en commun intermédiaire, avant même de vérifier avec les élèves si la tâche a été réalisée ou non, a énormément d’importance : elle permet d’interroger les stratégies utilisées par les élèves. Est-il possible de réussir ce que je vous ai demandé en procédant de cette manière ? En posant cette question, le maître lève ce que l’on appelle le malentendu scolaire (Cf. Elisabeth Bautier, in RFP #172) et permet aux élèves de bien différencier la tâche à réaliser (à savoir ici, se passer des sacs en indiquant ce qu’ils contiennent) des apprentissages que vise l’enseignant en proposant cette activité (à savoir, conduire vers l’abstraction de la notion de quantité).
Un autre but de la mise en commun intermédiaire est d’amener les élèves à dire ce qu’ils ont fait, c’est le début de la parole argumentative, un premier pas vers la conversation.
Enfin, l’activité se termine par une explicitation pour les élèves de l’apprentissage visé par le maître. En répondant à la question Pourquoi vous ai-je demandé de faire ça ? Qu’avez-vous appris en faisant cela ? les élèves sont ramenés au contexte de la classe et de l’école. Négliger cette étape, c’est passer à côté de l’acte d’enseigner, et pour l’élève, passer à côté de son métier d’élève.

D’autres activités, décrites dans l’ouvrage de M. Emprin et disponibles sur le site compagnon de ce livre, poursuivent également cet objectif :

• Mystéro
• La lecture de l’album Dans la cour de l’école de Christophe Loupy
• La lecture de l’album 1, 2, 3 petits chats qui savaient compter jusque 3 de Michel Van Zeveren

Ne jamais perdre de vue que ces activités permettent de réaliser ce que les programmes de 2015 disent ainsi :

Comprendre la notion de quantité implique pour l’enfant de concevoir que la quantité n’est pas la caractéristique d’un objet mais d’une collection d’objets (l’enfant doit également comprendre que le nombre sert à mémoriser la quantité) […] Le nombre en tant qu’outil de mesure de la quantité est stabilisé quand l’enfant peut l’associer à une collection, quelle qu’en soit la nature, la taille des éléments et l’espace occupé : cinq permet indistinctement de désigner cinq fourmis, cinq cubes ou cinq éléphants.

Qu’est-ce que connaître le nombre ?

Le nombre est un concept. On croit souvent à tort que le concept est maîtrisé par l’élève quand le langage associé à ce concept, l’est. Or un concept n’est pas que langage, selon G. Vergnaud, quatre éléments définissent un concept :

• Le langage et les représentations verbales ou non qui le symbolisent (par exemple, pour le nombre, les chiffres, les constellations organisées…)
• Les définitions et les propriétés utilisées implicitement ou explicitées
• Les résultats, les procédures, que suppose l’utilisation du concept. Ces procédures sont alors à automatiser ou – pour le moins – à savoir élaborer
• Les problèmes que l’utilisation de ce concept permet de résoudre

Quels sont alors les problèmes que l’utilisation du nombre (comme concept) permet de résoudre ? Répondre à cette question revient à se demander à quoi sert le nombre ? Il sert à :

• mémoriser une quantité
• comparer des quantités, deux collections
• anticiper des situations que l’on ne peut reproduire en vrai : par exemple, pour savoir combien la classe a mangé de gâteaux depuis le début de la semaine, on sera bien obligé d’utiliser le concept de nombre, puisqu’on a mangé les gâteaux ! Impossible de les recompter !

Cela étant dit, quelles situations-problème mettre en place dans la classe pour que les élèves soient amenés à construire la notion de nombre ? M. Emprin propose ici plusieurs activités :

• Le problème des pinceaux de Brousseau, où l’on demande à un élève de réaliser une collection équipotente à une collection qu’il n’a plus sous les yeux. La situation est connue. Elle fonctionne, à condition que, dans la consigne, l’enseignant ne dévoile pas la solution au problème et n’utilise donc pas les mots nombres, combien, quantité, compter…
• D’autres situations sont proposées dans l’ouvrage de M. Emprin et sur le site compagnon.
• Le nombre sert aussi à mémoriser une place, un ordre, un rang (c’est son aspect ordinal), d’où la situation dite Des trains  ou Des wagons où l’on va demander aux élèves d’indiquer à d’autres élèves dans quel wagon du train se trouve un objet qu’on y a caché. Il sera là encore forcé de construire les notions de premier, deuxième… wagon numéro sept.

Nous l’avons vu plus haut, la construction du concept implique celle de stratégies et de procédures auxquelles il faudra entraîner les élèves. Les Tice sont alors d’un grand secours pour l’enseignant, car la machine sait très bien répéter cent fois les mêmes choses ou aiguiller l’élève vers des exercices d’entrainement qui lui seront plus adaptés (si…, alors…) Pour cet usage, les logiciels Abuledu sont très efficaces et correspondent presque exactement aux situations de classe présentées ici. Ils sont gratuits et téléchargeables ici : logiciels Abuledu pour Windows.

Enfin, le jeu de l’Awale permet de s’exercer à utiliser le nombre pour anticiper en faisant appel à l’aspect cardinal ainsi qu’ordinal :

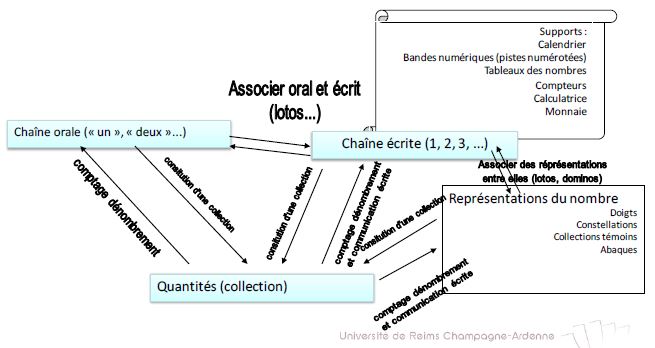
Pour résumer, le concept de nombre s’acquiert en réalisant des activités permettant de passer de la chaîne orale à la chaîne écrite, de la chaîne écrite à la quantité, de la quantité à la chaîne orale ou écrite. Dans tous les sens et réciproquement. Comme le montre le schéma ci-après :

Comment aborder des quantités plus importantes ? Apprendre à compter.

Mais à l’école, on ne saurait se contenter des collections qui peuvent se dénombrer par subitizing. Il faudra bien – une fois que le concept de nombre est bien installé chez l’élève – lui apprendre à compter des quantités plus importantes. Comment le faire ? Pour répondre à cette question, il faut se poser celle-ci : comment fais-je, moi, adulte, pour compter ? Ce faisant, nous mettrons en évidence deux compétences sous-jacentes et préalable à la compétence de comptage-dénombrement :

Savoir énumérer

Avant de savoir compter, il faut savoir :

• savoir énumérer, c’est à dire être capable de pointer une et une seule fois tous les éléments de la collection. C’est ce que permet d’acquérir une situation comme celle des boîtes d’allumettes, où l’on demande à l’enfant de mettre une et une seule allumette dans chacune des boîtes, le forçant ainsi à organiser la collection de boîtes entre celles dans lesquelles il y a déjà une allumette et celles encore à remplir. On ne parle pas ici de quantité ni de nombre, mais on apprend à énumérer.
  
• Organiser visuellement la collection à dénombrer, quand les objets ne sont pas déplaçables (comme le nombre de dents d’une roue dentée affichée loin de soi). Là encore, M. Emprin propose des activités telles que la bien connue Boîte à œufs où l’on demande aux enfants de placer un jeton dans chaque alvéole d’une plaque d’œufs, celle-ci étant cachée par un couvercle opaque ne permettant pas de voir quelle alvéole est déjà remplie…
• Les variables de ces activités sont :
  • Est-ce que les objets sont déplaçable ou non ?
  • La collection est-elle organisée (linéairement, en colonnes…) ou non ?
  • Peut-on marquer les objets ?
  • La différence entre la collection à énumérer et le nombre de jetons que l’on va proposer aux élèves.

Les albums à compter

Les albums à compter sont également une aide utile pour accéder aux nombres. Il existe de toutes sortes, Dominique Valentin en a fait une liste non exhaustive permettant, pour chaque album, de cibler les apprentissages particuliers (dénombrement, décomposition, de un en un, en avançant, en reculant…). Vous retrouverez son travail ici (attention, il date tout de même de 1992, la liste des publications est sans doute à réactualiser) : liste des albums à compter de Dominique Valentin, in Revue Grand N, n°52.

Pour aller plus loin

Un rallye mathématique à l’école maternelle ? Oui, c’est possible !

Chaque école de la circonscription dispose désormais de l’ouvrage cité dans cet article. Sachez qu’il s’accompagne d’un site web qui présente encore plus d’activités, de fiches de préparation et des séquences vidéos pour vous aider à les mettre en œuvre dans votre classe. C’est gratuit et ça n’engage à rien.

Le site compagnon de l’ouvrage Un rallye mathématique à l’école maternelle ? Oui, c’est possible ! : http://www.cndp.fr/crdp-reims/index.php?id=836

Trois questions à Fabien Emprin :

• Quels types de problèmes mathématiques les élèves de cycle 1 sont-ils capables de résoudre ?
• Qu’est-ce qu’un problème ouvert et comment définir une démarche pour le résoudre ?
• Pourquoi le repérage dans l’espace est-il important pour la résolution de problèmes au cycle 1 ?

Retrouvez ici et en vidéo les réponses de Fabien Emprin à ces trois questions :

http://www.cndp.fr/crdp-reims/ressources/conferences/fe05012011/emprin.htm